A Kármán–Howarth–Monin equation for variable-density turbulence

Abstract

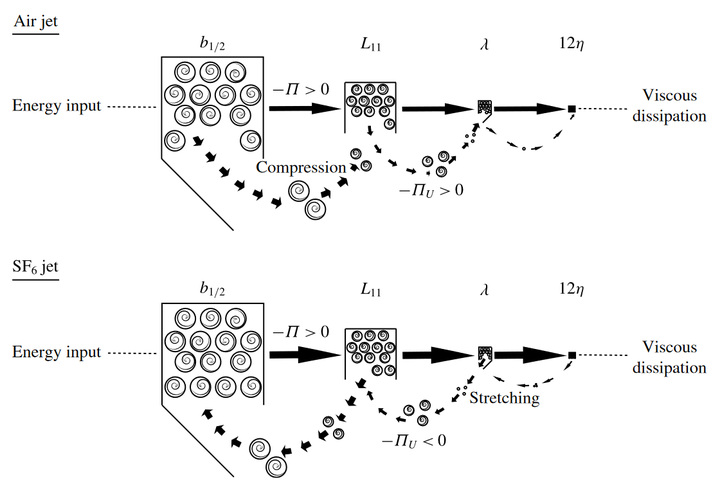
We present a generalisation of the Kármán–Howarth–Monin (K–H–M) equation to include variable-density (VD) effects. The derived equation (i) reduces to the original K–H–M equation when density is a constant and (ii) leads to a VD analogue of the 4/5-law with the same value of constant (=4/5) appearing as the prefactor of the dissipation rate. The equation is employed to understand negative turbulent kinetic energy production in a SF$_{6}$ turbulent round jet with an initial density ratio of 4.2. From a Reynolds-averaged Navier–Stokes (RANS) perspective, negative production means that the mean flow is strengthened at the expense of the energy of turbulent fluctuations. We show that the associated energy transfer is accomplished by the deformation of smaller turbulent eddies into large ones in the development region of the jet and is captured by the linear scale-by-scale energy transfer term in the VD K–H–M equation. The nonlinear transfer term of the VD K–H–M equation depicts a conventional forward cascade for all eddies having a size less than the Eulerian integral length scale, regardless of their orientation. The net effect is a retarded energy cascade in the non-Boussinesq jet that has not been accounted for by existing turbulence theories. Implications of this observation for turbulence modelling are discussed.